Brachistochrone Problem

The problem objective is to find the shape of a slope connecting two points, such that a ball rolling down the slope (from the higher to lower point) would do so in the shortest time. The gif (taken from nilabhasaha.wordpress.com) attached below illustrates this concept, using three curves: the path of shortest distance, the path of highest maximum acceleration and the brachistochrone.

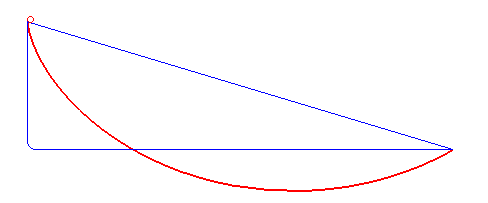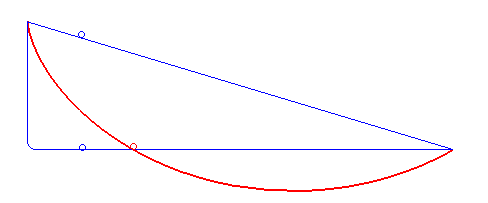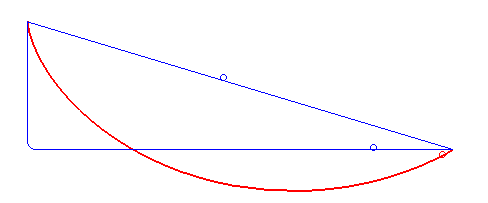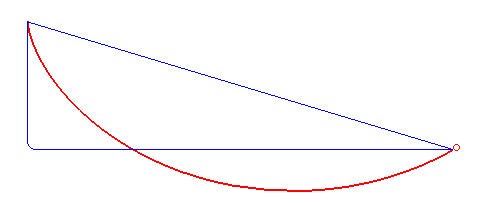
The mathematics I will use to solve this problem requires some understanding of matrix calculus, which I discuss in another article.

Defining Problem Parameters

I define the fixed end points to be $(0,0)$ to $(L,-H)$ and the slope to be $y(x)$. There is an implicit assumption that $y$ is somewhat well-behaved.

Here, $y \in \mathcal{V}$ where $\mathcal{V}$ denotes the vector space of functions defined on the range $[0,L]$

Quantifying the Time of Descent

We wish to determine the minimum value of a functional $T: \mathcal{V} \rightarrow \mathbb{R}$. To quantify the time of descent, $T$, we need to perform the integral

\[T(y) = \int _0 ^T \mathrm{d}t,\]

where $\mathrm{d}t$ is a minute timestep. We can calculate $\mathrm{d}t$ as

\[\mathrm{d}t = \frac{\mathrm{d}s}{v}.\]

It appears as though we have added more problems for ourselves! However, we can apply the conservation of energy to find v, as shown below,

\[mg \Delta h = \frac{1}{2}mv^2,\] \[v = \sqrt{2g \Delta h}.\]

From our definitions of the problem parameters, i.e. the start and end points of the slope,

\[\implies \Delta h = -y,\] \[\therefore v = \sqrt{-2gy}.\]

The next piece of the puzzle is to determine $\mathrm{d}s$, but this is just an infinitesimal increment of the arc length, and so can be given by the standard formula,

\[\mathrm{d}s = \sqrt{1 + y'^2}\mathrm{d}x.\]

This gives us the final formula for $T$,

\[T(y) = \int _0 ^L \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}}\; \mathrm{d}x.\]

Functional Differentiation

What we really wish to aquire is $\nabla _y T$ and set it equal to 0 for the minimum $T$. To do this, we utilise a concept from matrix calculus,

\[\mathrm{d}f = \nabla f(x) \cdot \mathrm{d}x.\]

and we generalise the inner/dot product to the Hilbert space of functions defined and well-behaved in $[0,L]$. We define the inner product of $u,v \in \mathcal{V}$ to be,

\[\langle u,v \rangle = \int _0 ^L uv\; \mathrm{d}x.\]

Now, let us use this in calculating $\nabla _y T$,

\[\mathrm{d}T = T(y+dy) - T(y).\]

The following steps substitute the formula for $T$ in and perform algebraic simplification,

\[\mathrm{d}T = \int _0 ^L \left[ \frac{\sqrt{1 + (y + \mathrm{d}y)'^2}}{\sqrt{-2g(y+\mathrm{d}y)}} - \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \right] \; \mathrm{d}x,\] \[\mathrm{d}T = \int _0 ^L \left[ \frac{\sqrt{1 + y'^2 + 2y'\mathrm{d}y' + \mathrm{d}y'^2}}{\sqrt{-2g(y+\mathrm{d}y)}} - \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \right] \; \mathrm{d}x.\]

Here we find ourselves with a differential squared, which goes to 0, because when considering derivatives, we only care about the linear term.

\[\mathrm{d}T = \int _0 ^L \left[ \frac{\sqrt{1 + y'^2 + 2y'\mathrm{d}y'}}{\sqrt{-2g(y+\mathrm{d}y)}} - \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \right] \; \mathrm{d}x,\] \[\mathrm{d}T = \int _0 ^L \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \left[ \left(1 + \frac{2y'\mathrm{d}y'}{1+y'^2}\right)^{1/2}\left(1+\frac{\mathrm{d}y}{y}\right)^{-1/2} - 1 \right] \; \mathrm{d}x.\]

The equation now begs for binomial expansion to be used upon it, so we will take the hint and proceed,

\[\mathrm{d}T = \int _0 ^L \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \left[ \left(1 + \frac{y'\mathrm{d}y'}{1+y'^2}\right)\left(1-\frac{\mathrm{d}y}{2y}\right) - 1 \right] \; \mathrm{d}x,\] \[\mathrm{d}T = \int _0 ^L \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \left[ \left(1 + \frac{y'\mathrm{d}y'}{1+y'^2}-\frac{\mathrm{d}y}{2y} + \mathcal(O)(dy'^2)\right) - 1 \right] \; \mathrm{d}x.\]

Again, we discard the second order $dy’^2$ terms,

\[\mathrm{d}T = \int _0 ^L \frac{\sqrt{1 + y'^2}}{\sqrt{-2gy}} \left[\frac{y'\mathrm{d}y'}{1+y'^2}-\frac{\mathrm{d}y}{2y}\right] \; \mathrm{d}x,\] \[\mathrm{d}T = \int _0 ^L \frac{y'\mathrm{d}y'}{\sqrt{1+y'^2}\sqrt{-2gy}} \; \mathrm{d}x - \int _0 ^L \frac{\sqrt{1 + y'^2}\mathrm{d}y}{2y\sqrt{-2gy}}\; \mathrm{d}x,\]

We wish to acquire something of the form, $\nabla _y T \cdot \mathrm{d}y = \int _0 ^L \nabla _y T \mathrm{d}y \mathrm{d}x$, so we employ integration by parts on the left hand term,

\[\mathrm{d}T = \left[ \left(\frac{y'}{\sqrt{1+y'^2}\sqrt{-2gy}}\right) \mathrm{d}y \right] _0 ^L - \int _0 ^L \left(\frac{y'}{\sqrt{1+y'^2}\sqrt{-2gy}}\right)' \mathrm{d}y \; \mathrm{d}x - \left[\frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}} \cdot \mathrm{d}y\right].\]

At $x = 0$ and $x = L$, we have defined fixed co-ordinates of $(0,0)$ and $(L,-H)$, and so any slight change in $y$ cannot change the values of $y(0)$ and $y(L)$, i.e. $dy(0) = dy(L) = 0$. Applying this removes the first term,

\[\mathrm{d}T = - \int _0 ^L \left(\frac{y'}{\sqrt{1+y'^2}\sqrt{-2gy}}\right)' \mathrm{d}y \; \mathrm{d}x - \left[\frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}} \cdot \mathrm{d}y\right],\] \[\mathrm{d}T = - \left[\left(\frac{y'}{\sqrt{1+y'^2}\sqrt{-2gy}}\right)' + \frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}}\right] \cdot \mathrm{d}y,\] \[\therefore \nabla _y T = - \left[\left(\frac{y'}{\sqrt{1+y'^2}\sqrt{-2gy}}\right)' + \frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}}\right].\]

Constructing the Governing Differential Equation

To find the minimum T, we now need to find where $\nabla _y T = 0$, i.e.

\[\left(\frac{y'}{\sqrt{1+y'^2}\sqrt{-2gy}}\right)' + \frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}} = 0.\]

Applying the quotient rule on the first term,

\[\frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}} = -\frac{y''\sqrt{(1+y'^2)(-2gy)} - y'\left( \frac{\sqrt{-2gy}}{\sqrt{1+y'^2}}y'y'' - \frac{\sqrt{1+y'^2}}{\sqrt{-2gy}}gy' \right)}{(1+y'^2)(-2gy)},\] \[\frac{\sqrt{1 + y'^2}}{2y\sqrt{-2gy}} = -\frac{y''(1+y'^2)(-2gy) - y'^2\left( -2gyy'' - (1+y'^2)g \right)}{\left[(1+y'^2)(-2gy)\right]^{3/2}},\] \[\frac{(1 + y'^2)^2}{2y} = \frac{y''(1+y'^2)(-2gy) + y'^2\left( 2gyy'' + (1+y'^2)g \right)}{2gy},\] \[(1 + y'^2)^2 = -2yy''(1+y'^2) + y'^2\left( 2yy'' + (1+y'^2) \right),\] \[\therefore 1 + 2yy'' + y'^2 = 0.\]

We merely need to solve this differential equation for $y$, or some condition of $y$. It turns out that this equation is non-trivial to solve and instead we take the approach of validating the true solution.

It can be proved via other methods that the brachistochrone must hold the form of a cycloid, which has governing equations,

\[x = a(\theta - \sin \theta)\] \[y = a(1 - \cos \theta)\]

if passing through the origin. Using chain rule, we can state that $\frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\mathrm{d}y/\mathrm{d}\theta}{\mathrm{d}x/\mathrm{d}\theta}$, and this is calculated below,

\[\frac{\mathrm{d}y}{\mathrm{d}\theta} = a \sin \theta,\] \[\frac{\mathrm{d}x}{\mathrm{d}\theta} = a (1 - \cos \theta),\] \[\implies y' = \frac{\sin \theta}{1 - \cos \theta}.\]

A similar rule can be applied to find $y’’$,

\[y'' = \frac{\mathrm{d}y'/\mathrm{d}\theta}{\mathrm{d}x/\mathrm{d}\theta},\] \[\frac{\mathrm{d}y'}{\mathrm{d}\theta} = \frac{\mathrm{d}}{\mathrm{d}\theta} \left[\frac{\sin \theta}{1 - \cos \theta}\right].\]

Applying the quotient rule allows us to progress further,

\[\frac{\mathrm{d}y'}{\mathrm{d}\theta} = \frac{\cos \theta (1 - \cos \theta) - \sin^2 \theta}{(1 - \cos \theta)^2},\] \[\frac{\mathrm{d}y'}{\mathrm{d}\theta} = \frac{\cos \theta - 1}{(\cos \theta - 1)^2} = \frac{1}{\cos \theta - 1},\] \[\implies y'' = -\frac{1}{a(1 - \cos \theta)^2}.\]

Now let us substitute these expressions for $y’’, y’$ and $y$ into the differential equation.

\[y'^2 + 2yy'' = -1.\] \[\frac{\sin \theta}{1 - \cos \theta}^2 - 2a(1 - \cos \theta)\frac{1}{a(1 - \cos \theta)^2} = -1.\]

Here, I invert all the negative signs to make subsequent calculations easier,

\[\frac{2}{(1 - \cos \theta)} - \frac{\sin \theta}{1 - \cos \theta}^2 = 1,\] \[\frac{2 - 2\cos\theta - \sin^2 \theta}{(1 - \cos\theta)^2} = 1,\] \[\frac{1- 2\cos\theta + \cos^2 \theta}{(1 - \cos\theta)^2} = 1,\] \[\frac{(1 - \cos\theta)^2}{(1 - \cos\theta)^2} = 1.\] \[\square\]

Since we have now shown the cycloid to be a valid solution of the differential equation, the next step is to calculate the parameters, i.e. we need to fit the curve to pass through the origin and $(L, -H)$. The starting point has already been dealt for us, so all that is left is to fit it to the end point. This is, however, a matter of solving two fairly non-trivial simultaneous equations. Instead of solving, I have listed the equations below, since this would be a far easier job if done numerically.

\[L = a(\theta - \sin \theta)\] \[-H = a(1 - \cos \theta)\]

21/07/2024