Donut

The task in this project was to develop a program that displays a rotating donut in console, using ascii characters. On this webpage, I have used javascript to render the program to work in the webpage. I attempted this project to study C++ and learn the ropes of the std library.

You can download the raw C++ file here. However, the code is displayed below, with descriptive text added throughout. For a full rundown, the originator of this project wrote an article describing the in-depth mathematics behind the donut. I used some of their pseudocode for inspiration.

The Code

// This project aims to program a rotating torus animation using ascii characters.

// Coy Zhu - 07/2024

// Include packages and define constants
#include <iostream>
#include <cmath>
#include <Eigen/Dense>
#include <string>
#include <cstdlib>
#include <vector>
#include <chrono>
#include <thread>
#include <array>
#include <omp.h>

In the following section, I use macros to define some constants.

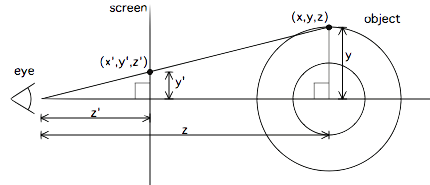
R1 denotes the minor radius and R2 the major radius of the torus. z1 gives the distance to the center of the torus from the origin and z0 the distance from origin to the projecting screen.

I also define a data structure to make for ease of data transfer between functions later.

#define screen_width 100
#define screen_height 100
#define R1 1
#define R2 2.0
#define z1 4
#define PI 3.14159265358979323846
constexpr double z0 = screen_width * z1 * 3 / (8 * (R1 + R2));


// Define structures
struct vector_scalar {
	std::vector<double> vector;
	double scalar;
};

The projection works as per the diagram shown below. We store the reciprocal of z so to determine the distance of the point from the origin. Later, we will compare the reciprocal of z to determine whether to display a pixel or not. r1 represents the coordinates on the projected screen.

// Define projection function
vector_scalar point_projection(double x, double y, double z) {
	double X, Y, ooz;

	X = x * z0 / (z + z1);
	Y = y * z0 / (z + z1);
	ooz = 1 / z;
	std::vector<double> r1 = { X,Y };

	vector_scalar r1ooz = { r1, ooz };

	return r1ooz;
}

I define the pixel positions for the surface of the torus. The expressions were determined using matrix multiplications of several rotation matrices and the locus of one single cross-sectional circle of the torus.

// Define the pixel function
std::vector<double> position(double theta, double phi, double A, double B) {
	double X, Y, Z;

	// Pre-calculating trig values
	double cosphi, sinphi, costheta, sintheta, cosA, sinA, cosB, sinB;
	cosphi = cos(phi);
	sinphi = sin(phi);
	costheta = cos(theta);
	sintheta = sin(theta);
	cosA = cos(A);
	sinA = sin(A);
	cosB = cos(B);
	sinB = sin(B);

	// Calculating the position components
	X = (R2 + R1 * costheta) * (cosphi * cosA + sinphi * sinA * sinB) + R1 * sintheta * sinA * cosB;
	Y = (R2 + R1 * costheta) * (sinphi * cosA * sinB - cosphi * sinA) + R1 * sintheta * cosA * cosB;
	Z = (R2 + R1 * costheta) * sinphi * cosB - R1 * sintheta * sinB;

	// Assigning components to a vector r
	std::vector<double> r = { X,Y,Z };
	return r;
}

The illumination index is defined similarly to the pixel positions but instead the matrices are used to find the normal surface vectors. Then, we dot the surface vectors with the light source direction to calculate an index.

// Illumination
double illumination(double theta, double phi, double A, double B) {
	double Nx, Ny, Nz, L;

	// Pre-calculating trig values
	double cosphi, sinphi, costheta, sintheta, cosA, sinA, cosB, sinB;
	cosphi = cos(phi);
	sinphi = sin(phi);
	costheta = cos(theta);
	sintheta = sin(theta);
	cosA = cos(A);
	sinA = sin(A);
	cosB = cos(B);
	sinB = sin(B);

	// Calculating the surface normal components
	Nx = cosA * cosphi * costheta + sinA * cosB * sintheta + sinA * sinB * costheta * sinphi;
	Ny = cosA * cosB * sintheta - sinA * cosphi * costheta + cosA * sinB * costheta * sinphi;
	Nz = cosB * costheta * sinphi - sinB * sintheta;

	// Assigning components to vector n
	Eigen::Vector3d n = { Nx, Ny, Nz };

	// Dot product n with the source direction for an illumination index
	Eigen::Vector3d src = { 0,-1,1 };
	L = n.dot(src);
	L /= sqrt(2);
	return L + 1;
}

Here, we form a large 2D array to represent each pixel on the projected screen, and calculate what ascii character to display at each pixel, given the reciprocal of z and the illumination index. The frame is then displayed by printing into console, and then clearing the display, followed by reprinting.

// Frame Rendering
void frame(double A, double B) {
	// Local variable declarations
	std::vector<double> r, r1;
	double ooz, L, theta, phi;
	vector_scalar r1ooz;

	// Initialise output array for storing the ascii characters to display
	static std::array<std::array<char, screen_width>, screen_height> output;
	std::memset(output.data(), ' ', sizeof(char) * screen_width * screen_height);

	// Potential double buffering
	/*char buffer[screen_width][screen_height];
	memset(buffer, ' ', sizeof output);*/

	// Initialise Z buffer to determine whether the point would be visible to us or not
	std::array<std::array<double, screen_width>, screen_height> z_buffer;
	std::memset(z_buffer.data(), 0, sizeof(double) * screen_width * screen_height);


	// Loop over theta and phi for the full toroid surface and calculate illumination values, storing results in buffer
	#pragma omp parallel for collapse(2)
	for (double theta = 0; theta < 2 * PI; theta += 0.05) {
		for (double phi = 0; phi < 2 * PI; phi += 0.01) {
			r = position(theta, phi, A, B);
			r1ooz = point_projection(r[0], r[1], r[2]);
			r1 = r1ooz.vector;
			ooz = r1ooz.scalar;
			int xp, yp;
			xp = round(screen_width / 2 + r1[0]);
			yp = round(screen_height / 2 + r1[1]);
			if (xp >= 0 && xp < screen_width && yp >= 0 && yp < screen_height) {
				L = illumination(theta, phi, A, B);
				if (L > 0 && ooz > z_buffer[xp][yp]) {
					z_buffer[xp][yp] = ooz;
					int index = round(L * 5.5);
					output[xp][yp] = ".,:;!-~=*#$@"[index];
				}
			}
		}
	}
	// Display frame
	std::cout << "\033cls";
	for (int j = 0; j < screen_height; j++) {
		for (int i = 0; i < screen_width; i++) {
			std::cout << output[i][j];
		}
		std::cout << std::endl;
	}
	// Could add double buffering
}

The main loop increments A and B for the animation movement, and adds a sleep timer.

// Main
int main() {
	double A, B;
	A = 0;
	B = 0;
	while (true) {
		frame(A, B);
		std::this_thread::sleep_for(std::chrono::milliseconds(1));
		A += 0.2;
		B += 0.3;
	}
}

16/07/2024